The Point3D module
Also see :
| Quick Notes |
- Parametric Point Maps
- Objects, Attributes, Methods and Functions
- Introduction to Python
- Text editor (to enter Point3D code)
PR 28434 In parametrics, fixed how the Point3D module handles invalid inputs to the Point3D constructor and to the module functions MakePoint3D and MakePoint. Previously, the routines threw syntax errors but did so incorrectly so that it would appear as if the following statement had an exception. Now we throw TypeErrors and they are raised as the correct statement . (v7.3)
PR 31422 In parametrics implemented __eq__ and __ne__ for Uuid, Point3D, and Transform3D such that the following holds.
p = Point3D.Point3D()
q = Point3D.Point3D()
assert p == q
assert not p <> q
(v2015)
| The general form of a Point3D object is Point3D( x, y, z ) , which makes it similar to a point object, though each remain distinct object types. A number of methods, such as xxx.add_node() in the Layout3D module require a Point3D object and will not take a point object. Also be aware that, depending on the function or method for which it is specified as an argument, a Point3D object may be interpreted as being a point (an actual location), or a vector (a direction, not a location). |
p1 = Point3D(point object). Click here for information on how to declare a point object.
| Point3D() can take a point object (point1 in this example) as its argument. |
|
p1 = Point3D(x, y, z). The arguments x, y, z are floating point numbers corresponding to x, y, z global coordinates (in alphabetical order).
|
Point3D() can take three floating point values as arguments. These correspond to global x, y, z coordinates. |
p1 = Point3D(list or tuple). Lists and tuples are built-in Python objects. See Python books, web sites and tutorials to learn more about Python and its basic object types.
| Point3D() can take a list or a tuple as its argument. As this example of a list shows, only the first three floating point values are used. |
|
p1 .x returns the X global coordinate of p1, where p1 is a Point3D object . An X global coordinate is a floating point number in mm or inches, depending on the startup code Units(' ... ') .
|
p1.x returns the first argument (the X global coordinate) of the Point3D object that has the variable name p1. |
p1 .y returns the Y global coordinate of p1, where p1 is a Point3D object . A Y global coordinate is a floating point number in mm or inches, depending on the startup code Units(' ... ') .
|
p1.y returns the second argument (the X global coordinate) of the Point3D object that has the variable name p1. |
p1 .z returns the Z global coordinate (elevation) of p1, where p1 is a Point3D object . A Z global coordinate is a floating point number in mm or inches, depending on the startup code Units(' ... ') .
|
p1.z returns the third argument (the elevation) of the Point3D object that has the variable name p1. |
Angle(v1, v2) or v1.Angle(v2) returns the angle (a floating point number in radians) between the two vectors ( v1 and v2 ). The arguments v1 and v2 can be Point3D objects in the form Point3D(x, y, z) .
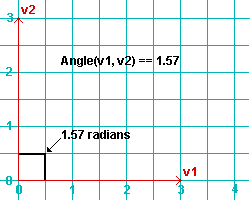
|
|
Bisector(v1, v2) or v1.Bisector(v2) returns a unit vector that bisects the two vectors, v1 and v2 , where v1 and v2 are Point3D objects . The unit vector is output in the form Point3D(x, y, z) , where the sum of the squares of x , y and z equal one ( x^2 + y^2 + z^2 = 1 ). For example, 0.7071**2 + 0.7071**2 is approximately 1.0 in the example below.
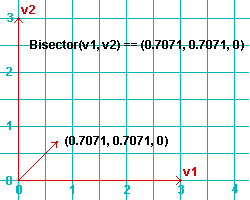
|
|
Cross(v1, v2) or v1.Cross(v2) returns the vector product of two vectors, v1 and v2 , where v1 and v2 are Point3D objects . The vector product is output in the form Point3D(x, y, z) .
| SDS2 Python Prompt |
|
>>> from Point3D import *
>>> v1 = Point3D(3, 0, 0) >>> v2 = Point3D(0, 3, 0) >>> Cross(v1, v2) Point3D(0, 0, 9) >>> print(Cross(v1, v2)) (0, 0, 9) |
Distance(p1, p2) or p1.Distance(p2) returns the distance between two points, p1 and p2 , where p1 and p2 are Point3D objects . A distance is a floating point number in mm or inches, depending on the startup code Units(' ... ') .
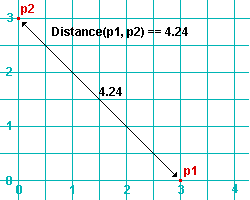
|
|
||
| Pythagoras would be quick to understand why Distance(p1, p2) gives the same result as sqrt(3*3 + 3*3). Also, note that p1 and p2 are both at elevation 0, and therefore are in the same plane, resulting in their Z coordinates not being used in the distance calculation. | |||
DistanceSquared(p1, p2) or p1.DistanceSquared(p2) returns the distance between two points, p1 and p2 , where p1 and p2 are Point3D objects . A distance is a floating point number in mm or inches, depending on the startup code Units(' ... ') .
| In this example, DistanceSquared(p1, p2) gives the same result as 3*3 + 3*3. Whereas DistanceSquared(p1, p3) gives the same result as 3*3 + 3*3 +3*3 |
|
Dot(v1, v2) or v1.Dot(v2) returns the scalar product between the two vectors, v1 and v2 , which are Point3D objects . This scalar product is equivalent to the product of the lengths of the vectors.
| SDS2 Python Prompt |
|
>>> from Point3D import *
>>> v000 = Point3D(0, 0, 0) >>> v222 = Point3D(2, 2, 2) >>> v333 = Point3D(3, 3, 3) >>> Dot(v222, v333) 18.0 >>> Distance(v000, v222) * Distance(v000, v333) 18.0 >>> Dot(v222, v333) == Distance(v000, v222) * Distance(v000, v333) True >>> Length(v222) * Length(v333) 18.0 >>> Dot(v222, v333) == Length(v222) * Length(v333) True |
EpsilonEquals(v1, v2, tolerance) or p1.EpsilonEquals(v2, tolerance) .
FloatEquals() is the same as EpsilonEquals() .
Interpolate(v1, v2, percent) or v1.Interpolate(v2, percent) returns a Point3D object that is the specified percentage of sum of the two vectors ( v1 + v2 ). The third argument ( percent ) is required and gives best results when less than 1.0.
|
In this example, the interpolated result is (75, 75, 75). Note that the mathematical expression
(50 + 100) * 0.5 also gives a result of 75. |
|
IsParallel(v1, v2) or v1.IsParallel(v2) returns True or False. The arguments v1 and v2 can be Point3D objects in the form Point3D(x, y, z) .

|
|
Isperpendicular(v1, v2) or v1.Isperpendicular(v2) returns True or False. The arguments v1 and v2 can be Point3D objects in the form Point3D(x, y, z) .
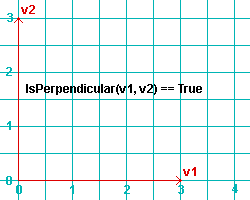
|
|
Length(v1) returns the length of the vector, v1 , where v1 is a Point3D object . Also see the example for Magnitude(v1) . Magnitude(v1) and Length(v1) are the same.
| Note, from the following example, that the length is equal to the distance between the origin (p000) and the point v1 (p000 + v1). | |||
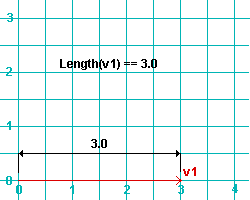
|
|
||
LengthSquared(v1) returns the square of the length of the vector, v1 , where v1 is a Point3D object .
|
Since v3 is (3, 3, 3) in this example,
LengthSquared(v3) gives the same result as the expression 3*3 + 3*3 + 3*3. |
|
Magnitude(v1) is the same as Length(v1) .
| In this example, the sqrt function is imported from the math module to produce the same result that is achived using Magnitude(s). |
|
ScalerProjection(v1, v2) returns the magnitude of the first vector ( v1 ) projected onto the second vector ( v2 ) and scaled according to the cosine of the angle between the two vectors. The arguments v1 and v2 can be Point3D objects in the form Point3D(x, y, z) .
|
In this example, the origin -- Math3D(0, 0, 0) -- and the vectors v111, v222 and v333 are equivalent, except for differences in magnitude (length) of 1.732 units. These differences in magnitude are not factored since the cosine of the angle between any of these vectors is 1.0
(i.e. cos 0 = 1). |
|
| In this next example, p111 and p_1_11 are no longer in line, but are 109.471 degrees from one another, resulting in the p_1_11 length being multiplied by the cosine of 109.471 degrees. | ||
|
Unit(v1) returns the unit vector of the vector v1 , where v1 is a Point3D object .
| A unit vector maintains the same ratio between its x, y and z coordinates as the ratio between coordinates in the original vector (v300 or v363 or v369). But the unit vector's coordinates are scaled so that their squares added together equal one. |
|







