The Math3D module
Also see :
| Quick Notes |
- Parametric Point Maps
- Objects, Attributes, Methods and Functions
- Introduction to Python
- Text editor (to enter Math3D code)
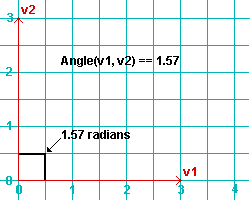
Angle(v1, v2) or v1.Angle(v2) returns the angle (in radians) between the two vectors ( v1 and v2 ). The arguments v1 and v2 can be Point3D objects in the form Point3D(x, y, z) .
|
|
|
AngleLinePlane((p, u), (q, n)) returns the angle (in radians) between the line (p, u) and the plane (q, n) , where p , u , q and n are all Point3D objects . For the (p, u) line, p is a point on the line, u is a vector that defines the direction of the line from p. For the (q, n) plane, q is a point on the plane, n is a vector that is normal to the plane.
| All points in the plane (q, n) are at an elevation of z = 0. The line (p, u) is at an angle of 45 degrees (0.785 radians) from that plane. |
|
AnglePlanes((p, u), (q, v)) returns the angle between plane (p, u) and plane (q, v) , where p , u , q and v are Point3D objects . For the (p, u) plane, p is a point on the plane, u is a vector. Similarly, for the ( q, v ) plane, q is a point, and v is a vector that sets the directions of the plane from that point.
| All points in the (p, u) plane are at an elevation of z = 5. Points in the (q, v) plane are in y = 5, making it perpendicular to the other plane. The angle between the planes is 1.5708 radians, which is 90 degrees. |
|
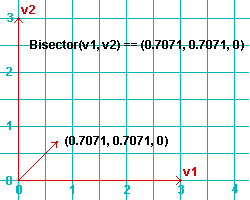
Bisector(v1, v2) returns a unit vector that bisects the two vectors ( v1 and v2 ). The arguments v1 and v2 can be Point3D objects . The unit vector is output in the form Point3D(x, y, z) , where the sum of the squares of x , y and z equal one ( x^2 + y^2 + z^2 = 1 ). For example, 0.7071**2 + 0.7071**2 is approximately 1.0 in the example below.
|
|
ClosestPointOnLine(p, (q, v)) returns the closest Point3D to the point p on line (q, v) , where p , q and v are all Point3D objects . For the (q, v) line, q is a point, and v sets the direction of the line with respect to that point.
| The line (p, v) is a vertical line comprised of points with 3, 3 coordinates at different elevations. The point closest to p on that line is Point3D(3, 3, 100). |
|
ClosestPointOnPlane(p, (q, n)) returns the closest Point3D to the point p that is on the plane (q, n) , where p , q and n are all Point3D objects . For the (q, n) plane, q is a point on the plane, and n is a vector that is normal to that plane.
| All points in the plane (q, n) are at an elevation of z = 5. The closest point on that plane to Point3D(11, 20, 10) is Point3D(11, 20, 5). |
|
ClosestPointsBetweenLines((p, u), (q, v), accy=0.0001) returns the closest Point3D on line (p, u) to line (q, v) and the closest Point3D on line (q, v) to line (p, u) , where p , u , q and v are Point3D objects . The third argument ( accy=some_number ) is optional; if omitted, the accuracy is 0.0001.
| The line (p, u) is a vertical line through the x, y coordinates 3, 3. (q, v) is a horizontal line that runs parallel to the y coordinate 3 at elevation 20. (r, v) is a horizontal line that runs parallel to the y coordinate 5 at elevation 20. |
|
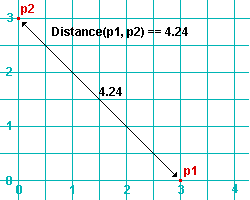
Distance(p1, p2) or p1.Distance(p2) returns the distance between the points p1 and p2 , where p1 and p2 are Point3D objects .
|
|
||
| Pythagoras would be quick to understand why Distance(p1, p2) gives the same result as math.sqrt(3*3 + 3*3) and math.hypot(3, 3). Also, note that p1 and p2 are both at elevation 0, and therefore are in the same plane, resulting in their Z coordinates not being used in the distance calculation. | |||
DistancePointLine(p, (q, v)) returns the distance between the point p and the line (q, v) , where p , q and v are all Point3D objects . For the (q, v) line, q is a point on the line, and v is the vector that sets the direction in which the line proceeds through that point.
| The line (q, v) is a vertical line through the x, y coordinates 5, 5. The point closest to p on that line is Point3D(5, 5, 100). The distance between those points is 5.0. |
|
DistancePointPlane(p, (q, n)) returns the distance that the point p is from the plane (q, n) , where p , q and v are all Point3D objects . For the (q, n) plane, q is a point on the plane, and n is a vector that is normal to that plane.
| All points in the plane (q, n) are at an elevation of z = 5. The closest point on that plane to Point3D(11, 20, 10) is Point3D(11, 20, 5). The distance between those points is 5.0. |
|
DistanceSquared(p1, p2) or p1.DistanceSquared(p2) returns the distance between two points ( p1 and p2 ), where p1 and p2 are Point3D objects .
|
In this example,
DistanceSquared(p1, p2) gives the same result as 3*3 + 3*3. Whereas DistanceSquared(p1, p3) gives the same result as 3*3 + 3*3 +3*3 |
|
Dot(v1, v2) returns the scalar product between the two vectors ( v1 and v2 ), which are Point3D objects . The scalar product is equivalent to the product of the lengths of the vectors.
| SDS2 Python Prompt |
|
>>> from Math3D import *
>>> v000 = Point3D(0, 0, 0) >>> v222 = Point3D(2, 2, 2) >>> v333 = Point3D(3, 3, 3) >>> Dot(v222, v333) 18.0 >>> Distance(v000, v222) * Distance(v000, v333) 18.0 >>> Dot(v222, v333) == Distance(v000, v222) * Distance(v000, v333) True >>> Length(v222) * Length(v333) 18.0 >>> Dot(v222, v333) == Length(v222) * Length(v333) True |
EpsilonEquals(v1, v2, tolerance) or p1.EpsilonEquals(v2, tolerance) .
FloatEquals() is the same as EpsilonEquals() .
Interpolate(v1, v2, percent) returns a Point3D object that is the specified percentage of sum of the two vectors ( v1 + v2 ). The third argument ( percent ) is required and gives best results when less than 1.0.
|
In this example, the interpolated result is (75, 75, 75). Note that
(50 + 100) * 0.5 is equal to 75.0. |
|
IntersectLinePlane((p, u), (q, n), accy=0.0001) returns the intersection of the line (p, u) and the plane (q, n) . It returns (p, u) if the line is on the plane. It returns (None, None) if the line does not intersect the plane. It returns (Point3D, None) if the line intersects the plane at one point. The third argument ( accy=some_number ) is optional; if omitted, the accuracy is 0.0001.
| The line (p, u) is a diagonal horizontal line at elevation z = 5. Points in the (q, n) plane are at elevation z = 5. The line (p1, u) is horizontal at z = 3 and parallel to (not intersecting) the plane. The line (p, v) is perpendicular to the plane and intersects it at 3, 3, 5. |
|
IntersectPlanes((p, v), (q, u), accy=0.0001) returns the intersection of two planes, (p, v) and (q, u) . It returns (None, None, None) if the planes don't intersect. It returns (Point3D, Point3D, None) if the planes intersect in a line. It returns (p, v) if the planes intersect in a plane. The third argument ( accy=some_number ) is optional; if omitted, the accuracy is 0.0001.
IsParallel(v1, v2) or v1.IsParallel(v2) returns True or False. The arguments v1 and v2 are Point3D objects .

|
|
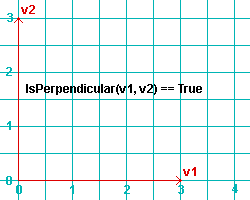
Isperpendicular(v1, v2) or v1.Isperpendicular(v2) returns True or False. The arguments v1 and v2 are Point3D objects .
|
|
Length(v1) returns the length of the vector ( v1 ), where v1 is a Point3D object . Also see the example for Magnitude(v1) . Magnitude(v1) and Length(v1) are the same.
| Note, from the following example, that the length is equal to the distance between the origin (p000) and the point v1 (p000 + v1). | |||
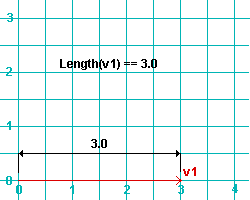
|
|
||
LengthSquared(v1) returns the square of the length of the vector ( v1 ), where v1 is a Point3D object .
|
Since v3 is (3, 3, 3) in this example,
LengthSquared(v3) gives the same result as the expression 3*3 + 3*3 + 3*3. |
|
Magnitude(v1) is the same as Length(v1) .
|
In this example,
math.sqrt(4*4 + 6*6) produces the same result as Magnitude(s). |
|
PlaneToPoint(p, (q, n)) returns the vector from the plane (q, n) to the point p , where p , q and n are Point3D objects . For the (q, n) plane, q is a point on the plane, n is a vector that is normal to the plane.
| Points in the (q, n) plane are at elevation z = 5. The point p is at z = 3, two units below the plane. The point p1 is at z = 7, two units above the plane. |
|
Point3D lets you define a Point3D object as described here , in the documentation for the Point3D module. The general form of a Point3D object is Point3D(x, y, z) .
| Key concept: Depending on the function or method for which it is specified as an argument, a Point3D object may be interpreted as being a point (in which case, it has an actual location), or a vector (in which case it a direction, not a location). In this documentation, p and q usually designate points, whereas v , u and n are vectors, with n being a vector that is normal to the plane. |
PointOnLineSegment(p, (l, r), accy=0.0001, l_inclusive=True, r_inclusive=True) returns True if p is on the line segment (l, r) , where p , l and r are Point3D objects . For the (l, r) line segment, l and r are its left and right end points. accy=some_number is optional; if omitted, the accuracy is 0.0001. l_inclusive=True/False and/or r_inclusive=True/False control whether the left and/or right end points are considered to be a part of the line; if both are omitted, the line segment is considered to include both end points (i.e., True is the default).
| SDS2 Python Prompt |
|
>>> from Math3D import *
>>> p = Point3D(3, 3, 3.0001) >>> l = Point3D(1, 1, 3) >>> r = Point3D(4, 4, 3) >>> PointOnLineSegment(p, (l, r)) True >>> PointOnLineSegment(p, (l, r), accy=0.01) True >>> PointOnLineSegment(p, (l, r), accy=0.00001) False >>> PointOnLineSegment(l, (l, r)) True >>> PointOnLineSegment(l, (l, r), l_inclusive=False) False |
PointOnPlane(p, (q, n), accy=0.0001) returns True if p is on the plane (q, n) , where p , q and n are Point3D objects . For the (q, n) plane, q is a point on the plane, and n is a vector that is normal to the plane. The third argument ( accy=some_number ) is optional; if omitted, the accuracy is 0.0001.
| All points in the (q, n) plane are y = 5 points. True is returned when point p is on that plane within the specified accuracy. |
|
PointToPlane(p, (q, n)) returns the vector from the point p to the plane (q, n) , where p , q and n are Point3D objects . For the (q, n) plane, q is a point on the plane, and n is a vector that is normal to the plane.
|
All points in the (q, n) plane are x = 5 points.
All points in the (q, n1) plane are x, y = 5, 5 points. |
|
ScalarProjection(v1, v2) returns the length of first vector ( v1 ) projected onto the second vector ( v2 ) and scaled according to the cosine of the angle between the two vectors. The arguments v1 and v2 can be Point3D objects in the form Point3D(x, y, z) .
|
In this example, the origin -- Math3D(0, 0, 0) -- and the vectors v111, v222 and v333 are equivalent, except for differences in magnitude (length) of 1.732 units. These differences in magnitude are not factored since the cosine of the angle between any of these vectors is 1.0
(i.e., cos 0 = 1). |
|
| In this next example, v111 and v_1_11 are not in line, but are 109.471 degrees from one another, resulting in the v_1_11 magnitude being multiplied by the cosine of 109.471 degrees. | ||
|
Unit(v1) returns the unit vector of the vector ( v1 ). The argument v1 can be a Point3D object in the form Point3D(x, y, z) .
| A unit vector maintains the same ratio between its x, y and z coordinates as the ratio between coordinates in the original vector (v300 or v363 or v369). But the unit vector's coordinates are scaled so that their squares added together equal one. |
|
math is a Python module that is imported when you import the Math3D module.
| Here are a few examples of some of the math methods that are available. Be aware that you can also import the math module directly, without importing the Math3D module. Use the dir() function to get help on the math module. |
|